La Curva de Koch

¿Qué dirías si supieras que a partir de un simple triángulo equilátero podemos obtener un maravilloso e increible Fractal? Quédate y descúbrelo...

El creador en 1904 de este monstruo fue Niels Fabian Helge von Koch, matemático sueco.

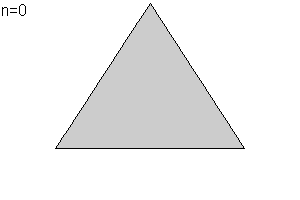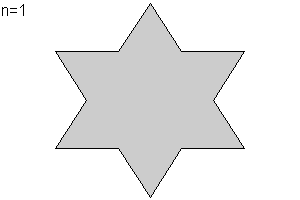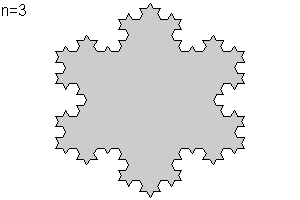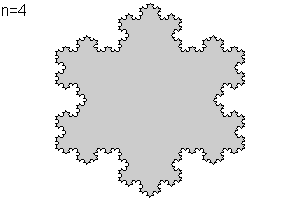
Partamos de un triángulo equilátero de lado unidad. Dividimos en tres partes iguales de longitud 1/3 cada lado. Sustituimos el segmento central por dos segmentos de tamaño idéntico formando un diente (n=1). Tenemos una curva poligonal P1 de longitud 3·4··1/3=4.

Repetimos la operación (n=2) con cada uno de los cuatro nuevos segmentos de cada uno de los "lados". Obtendremos así la curva P2 de longitud 3·4 elevado a 2 · 1/3 elevado a 2= 16/3. La iteración indefinida nos proporciona la isla de Koch o copo de nieve de Koch.

Existen diversas variantes sobre la construcción de la curva de Koch. Este modelo parte de un hexágono:

En este video también explica como es el proceso de la construcción del copo de nieve de Koch:

Para más información, consulta la página web de donde hemos tomado esta informción:

http://www.dmae.upm.es/cursofractales/capitulo1/2.html